Kafa Karıştırmasına Rağmen Çözülebilen Matematik Problemi: Lastik İp Üzerindeki Karınca
"1 km uzunluğundaki lastik bir ipin bir ucunda, diğer uca doğru -ipe göre- saniyede 1 cm hızla yürüyen bir karınca olsun. soru şu: ipin saniye başına homojen bir şekilde 1 km hızla uzadığı düşünülürse, söz konusu karınca diğer uca ulaşabilir mi?"

ant on a rubber rope (lastik ip üzerindeki karınca) problemi olarak bilinen bu sorunun cevabı (ipin uzama hızının karıncanın hızından daha fazla olması nedeniyle) ilk bakışta hayır olarak görünse de, aslında karıncanın -kendi hızından ötürü- ipe göre daha hızlı ilerlemesinden* ve de ipin, daha doğru bir ifadeyle ipin üzerindeki her noktanın eşit bir şekilde uzamasından dolayı** karınca (her ikisi de sabit olduğu sürece, karıncanın yürüme ve ipin uzama hızları ne olursa olsun) matematiksel anlamda eninde sonunda ipin diğer ucuna ulaşacaktır.
* karıncanın yere göre mutlak hızı = ipin yere göre hızı + karıncanın ipe göre hızı
** bunu soruyu biraz değiştirerek şöyle açıklayabiliriz: başlangıçta karınca ipin orta noktasına bırakılmış olsun ve ip yine uzamaya devam etsin. bu durumda karınca tamamen hareketsiz dahi olsa ip ne kadar çekilirse çekilsin, karıncanın yeri ipe göre oransal anlamda hep sabit olacak ve her daim ipin tam orta noktasında olacaktır. şimdi aynı konumda bu sefer karıncanın sabit bir hızla ilerlediğini düşünelim. bu yeni durumda ipin her uzamasında karınca orta noktaya göre çok çok ufak bir miktarda da olsa ilerlemiş olacak ve bu diferansiyel farklar integral hesabıyla toplandığında karınca çok uzun sürse de teorik olarak ipin sonuna varır.
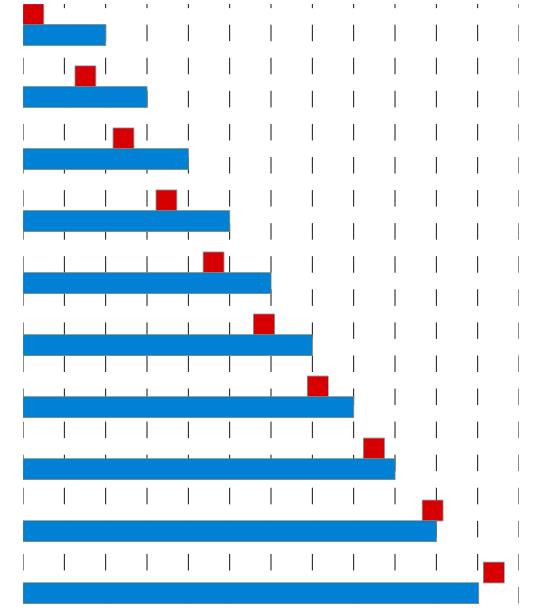
problemin matematiksel çözümleri
c = ipin başlangıçtaki uzunluğu,
v = ipin uzama hızı,
a = karıncanın ipe göre hızı
çözüm i.
b(t) = t zamanı sonunda karıncanın yürüdüğü toplam yolun, ipin toplam uzunluğuna oranı olacak şekilde bir b(t) belirleyelim. buna göre,
b(1) = a/(c+v) ---> ilk saniyenin sonunda, karınca ipe göre a birim yürümüşken, ip de yere göre toplamda c+v uzunluğuna ulaşmış olacaktır.
b(2) = a/(c+v) + a/(c+2v) ----------------> 1. ve 2. saniyeler arasında karınca ipe göre toplamda a birim yürümüş olsa da, ip yere göre toplamda c+2v uzunluğunda olacaktır.
.
.
.
b(n) = a/(c+v)+a/(c+2v)+...+a/(c+nv) ----------------> n-1. ve n. saniyeler arasında karınca ipe göre toplamda a birim yürümüş olsa da, ip yere göre toplamda c+nv uzunluğunda olacaktır.
şimdi yine n'nin fonksiyonu olacak şekilde yeni bir oran, d(n), tanımlayalım, öyle ki;
d(n) = a/(c+v)+a/(2c+2v)+...+a/(nc+nv) olsun. not: d(n)-d(n-1) = a/(c+v) x (1/n)
her a, c, v pozitif reel sayısı ve k doğal sayısı için cebirsel olarak,
a/(c+kv) >= a/(kc+kv) = (a/c+v) x (1/k) olacağından her koşulda b(n) >= d(n) olacaktır.
bu halde, b(n) >= d(n) = a/(c+v) x (1+1/2+...+1/n) eşitsizliği sağlanır.
(1+1/2+...+1/n) terimi matematikte harmonik seri olarak adlandırılır ve bu serinin toplamı sonsuza ıraksar. bu da b(t) oranını 1'den büyük (dolayısıyla da karıncanın katettiği toplam mesafenin ipin son uzunluğundan daha büyük olacağı, bir diğer ifadeyle karıncanın diğer uca varabileceği) yapacak bir m zamanına er geç ulaşılabileceği anlamını taşımaktadır:
m öyle ki, d(m) = harmonik(m) x a/(c+v) >=1 olacak şekilde
harmonik (m) = (1+1/2+...+1/m) >= (c+v)/a bulunur
ve nihayet, b(m) >= d(m) >= 1
not: bu sonuç, her ne kadar problemin cebirsel bir çözümü olduğunu gösterse de karıncanın hareket etmesi gereken toplam zamanı göstermez. söz konusu zaman, çözüm ii'de verilecektir.
çözüm ii.
karıncadan bağımsız düşünüldüğünde ipin uzama hızı sabit olmak kaydıyla ne kadar süre geçerse geçsin, ipin üstündeki bütün noktaların koordinatlarının başlangıç noktasından uzaklığı ipin toplam uzunluğa oranı sabit olacağından dolayı (ipin orta noktası her zaman orta nokta olarak kalacaktır), karıncanın başlangıç noktasına göre pozisyonunun ipin o anki toplam uzunluğuna oranı ile karıncanın ipe göre anlık hızının ipin yere göre hızına oranı birbirine eşittir ve bu iki oran da a/(c+vt) eşitliğiyle elde edilir.
karıncanın ipin t zamanındaki toplam uzunluk için anlık hızını e(t) = a/(c+vt) alırsak, aynı karıncanın ipin toplam uzunluğuna oranla anlık konumunu p(t) = e (t) x delta (t) = a/(c+vt) x delta (t) olarak hesaplayabiliriz. bu durumda delta(t) zaman değişimi sıfıra yakınsarken anlık diferansiyel yer değiştirme oranının toplamı integral hesabıyla bulunur:
p(t) = belirsiz integral (a/(c+vt) x dt) ---------->
p(t) = ((a/v) x ln (c+vt)) + k.
başlangıç koşulu olan p(0) = 0 için, k = -a/v x ln c bulunur.
o halde, p(t) = (a/v) x ln (c+vt/c).
diğer sınır koşulu olan p(s) = 1 eşitliğini sağlayan, başka bir ifadeyle karıncanın ipin ucuna ulaşacağı zaman olan s ise, p(s) = (a/v) x ln (c+vs/c) = 1 denklemi sayesinde
s = (c/v) x (e^(v/a)-1) olarak bulunur.
açıklama: karıncanın ipin ucuna ulaşabilmesi için gereken zaman, e sayısının iki hızın birbirine oranı kadar kuvveti (yani ipin uzama hızının karıncanın yürüme hızına oranı) ile doğru orantılıdır.
------------------------ sayısal örnekler:
örnek i.
ilk sorudaki hızlar göz önüne alındığında (ipin hızı 1 km/s, karıncanın hızı 1 cm/s), karınca ipin diğer ucuna 2,8 x 10^43429 saniyede ulaşacaktır. big bang'dan bu yana sadece 4 x 10^17 saniye geçtiği düşünüldüğünde, elde edilen değerin ne kadar devasa (ancak her şeye karşın sonlu) bir zamana tekabül ettiği anlaşılabilir.
örnek ii.
ipin başlangıç boyu 10 cm, uzama hızı 10 cm/s ve karıncanın yürüme hızı 1 cm/s için, geçmesi gereken zaman yaklaşık olarak 33616 saniyedir.
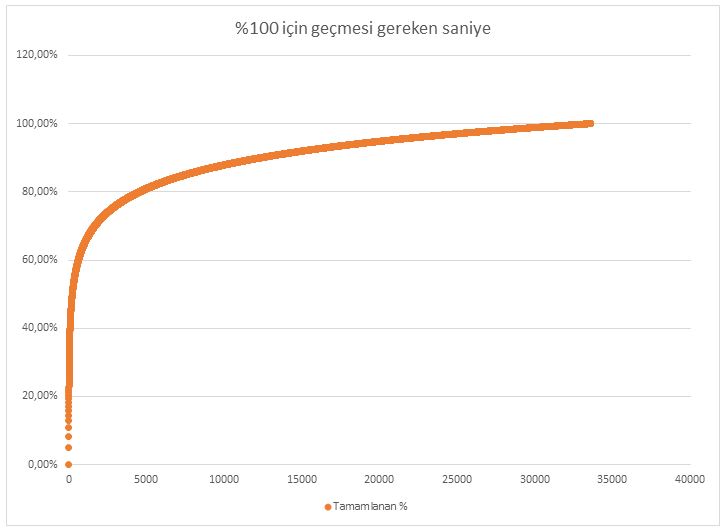
örnek iii.
ipin başlangıç boyu 3 cm, uzama hızı 3 cm/s ve karıncanın yürüme hızı 1 cm/s için, geçmesi gereken zaman yaklaşık olarak 30 saniyedir.
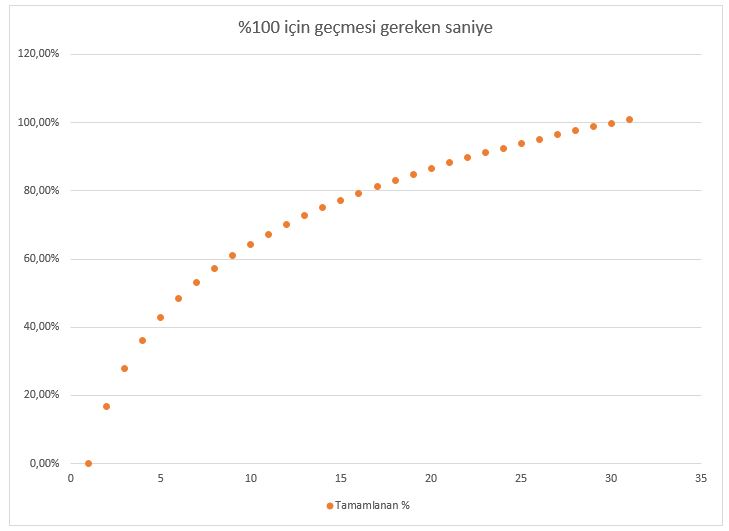
ekstra notlar
evrenle bir analoji kurmak gerekirse bu problem, ne kadar uzakta olursa olsunlar galaksilerin ışıklarının eninde sonunda bize ulaşıp ulaşamayacağı sorusunu da akla getirmekte. ancak gerek uzayın genişleme hızı ışık hızından fazladır anomalisi gerekse de uzayın genişleme hızının sabit olmayıp sürekli artması (ant on a rubber rope sorusunun çıkış noktası ilintili bütün hızların sabit olmasıydı) nedeniyle yeterince uzak galaksilerin ışıkları bize hiçbir zaman ulaşmayabilir.
ayrıca bakınız: (bkz: olbers paradoksu)
referanslar:
https://www.quora.com/…rubber-rope-paradox-possible
https://news.ycombinator.com/…t0p9njvd5q9coheg3lo24
https://www.science20.com/…me_farthest_scotty-99845
https://www.mlook.mobi/…61dedb124f53f5478c5a88a.pdf
https://www.youtube.com/watch?v=4k1jegu4wb4
https://www.youtube.com/watch?v=om9kepksg6u
https://en.wikipedia.org/wiki/ant_on_a_rubber_rope
https://www.theproblemsite.com/…math/2002/long-walk
https://www.iflscience.com/…-universe-accelerating/
https://www.sciencealert.com/…d-rate-say-physicists



